• Initial speed of rotation: n = 4000 min
-1
• Rotor inertia: J
R
= 4 kgcm
2
• Load inertia: J
L
= 6 kgcm
2
Calculation of the energy to be absorbed:
E
B
= 1/2 * J * (2*π*n * 1/60)
2
to 88 Ws
Electrical and mechanical losses are ignored.
In this example, the DC bus capacitors absorb 23 Ws (the value
depends on the device type, see chapter "2 Technical Data").
The internal braking resistor must absorb the remaining 65 Ws. It can
absorb a pulse of 80 Ws. If the load is decelerated once, the internal
braking resistor is sufficient.
If the deceleration process is repeated cyclically, the continuous out-
put must be considered. If the cycle time is longer than the ratio of the
energy to be absorbed E
B
and the continuous power P
PR
, the internal
braking resistor is sufficient. If the system decelerates more frequently,
the internal braking resistor is not sufficient.
In the example, the ratio E
B
/P
PR
is 1.3 s. If the cycle time is shorter, an
external braking resistor is required.
Selecting an external braking
resistor
The selection is made in two steps:
• The maximum energy during deceleration must be less than the
peak energy that the internal braking resistor can absorb:
(E
Di
)<(E
Cr
). In addition, the continuous power of the internal braking
resistor must not be exceeded: (P
C
)<(P
Pr
). If these conditions are
met, then the internal braking resistor is sufficient.
• If one of the conditions is not met, you must use an external brak-
ing resistor. The braking resistor must be rated in such a way that
the conditions are met. The resistance of the braking resistor must
be between the specified minimum and maximum values, since
otherwise the load can no longer be decelerated or the product
might be destroyed.
See chapter "2.3 Braking resistor", page 17 for technical data on the
external braking resistors.
LXM32
3 Engineering
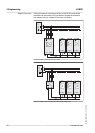
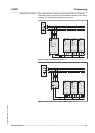
Common DC bus
35
MNA01M001EN, V1.01, 08.2014