BERT Technical Articles
B-34 GB1400 User Manual
That is, n is within
n
of the expected count most of the time (68% of the time). If we take the
inaccuracy of the measurement to be σ as a fraction of n, then
Inaccuracy
68%
= σ / n ≈ 1/
n
. (7a)
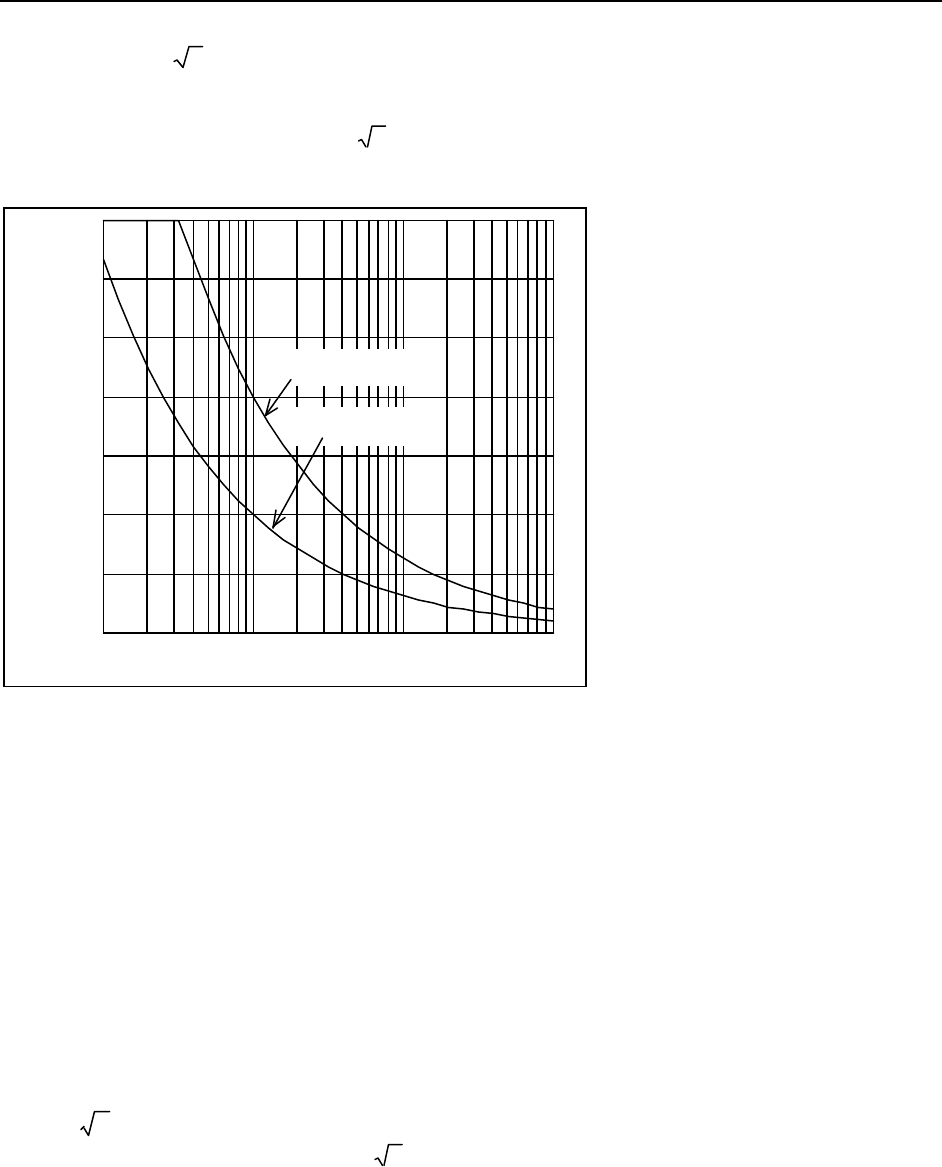
This relationship is plotted in Figure 3 (the curve for 68% confidence).
10
100 1000
10000
30
20
10
0
Inaccuracy
in %
Number of errors measured n
68% Confidence
95% Confidence
Figure 3. Inaccuracy error-rate measurement can be expressed as a function of the number of
errors measured. A confidence of 68 percent means that if the test is repeated, the measured error
rate will be closer to the actual error rate than inaccuracy indicated 68 percent of the time. For 95
percent confidence, the inaccuracy is twice as large.
As an example, suppose it is desired that the accuracy be 0.10, or 10%. Then from Eq. (7a) the test must
continue until n = 100. If the time to collect 100 errors turned out to be T = 19 hr, then r' = 100 / 19 hr =
5.26 / hr, and this is within 10% of the actual error rate r. That is, r is inferred to lie between 5.26 – 0.526
= 4.734 / hr and 5.26 + 0.526 = 5.78 / hr (with a confidence of 68%). Because of the statistical nature of
the measurement, n = 100 can be more than 10% away from the expected measurement, but 68% of the
time it will be less than 10% away.
You can increase your confidence level by using 2σ. The measured n = 100 is within 2σ (or 20% here) of
the expected count 95% of the time (see the other curve in Figure 3). In the example of r' = 5.26 / hr, r
is inferred to lie between 5.26 – 1.052 = 4.208 / hr and 5.26 + 1.052 = 6.312 / hr with a confidence of
95%. You are more confident the inaccuracy won't be exceeded, but the inaccuracy is twice as large.
To maintain a confidence of 95% (the higher curve in Figure 3) and still have an inaccuracy of 10%, you
need to count more errors. If 2σ is to be 10% of n, then σ is 5% of n, or σ / n = 0.05. From Eq.(6) this
gives 1 /
n
= 0.05, or n = 400. The general expression for the inaccuracy with 95% confidence is
Inaccuracy
95%
= 2σ / n ≈ 2/
n
. (7b)


















